利用IDL从TRMM/TMI卫星数据反演全球SST

发表于 | 分类于 | 阅读次数

实验目的：

  理论与实验课的综合运用，提高课堂与实践相结合的分析能力

  1. 了解海洋卫星反演SST的物理原理以及两种类型（热红外与微波辐射计）的卫星传感器；
  2. 熟悉TRMM/TMI；
  3. 掌握TMI反演SST的算法；
  4. 进一步熟悉IDL编程语言；
  5. 了解TMI的数据结构以及数据的输入与输出；
  6. 学会数据的图形显示，创建图形输出；
  7. 掌握数据的图象显示；
  8. 熟悉SST数据的读取，显示，输出，并注意colorbar的显示；
  9. 了解SST对全球气候的影响以及重要意义，着重说明SST全球分布的特点。

实验主要仪器设备，软件

  1. 硬件准备：PC机；
  2. 操作系统：Linux系统或Windows 2k以上系统；
  3. 软件开发工具：IDL语言
  4. 2012-2013年日、周、月均的TRMM/TMI二进制卫星数据

微波辐射计反演SST的原理介绍

  根据电磁辐射理论，辐射传输方程的微分形式是

$$ \dfrac { {\rm d}L\left( z\right) } { {\rm d}z}+L\left( z\right) K_{ab}=L_{B}\left( z\right) K_{ab} $$

  式中$L\left( z\right)$是在位置z处的辐亮度，$K_{ab}$是在传输路径上介质的吸收系数，$L\left( z\right) K_{ab}$是因大气中吸收气体的吸收而衰减的辐亮度，$L_{B}$是与吸收气体温度相同的黑体发射的辐亮度。由于微波波长远大于大气层中各种粒子的尺度，散射衰减对于微波影响一般可以忽略，而仅仅需要考虑吸收引起的衰减。利用瑞利-金斯定律，我们得到
$$T\left( \theta ,h\right) =etT_{s}+T_{u}\left( \theta ,h\right)etT_{s}+\int _{0}^{h}T\left( z\right)K_{ab}\left( z\right) e^{-\tau\left(z,h\right)sec\theta }sec\theta {\rm d}z$$
  式中$T\left( \theta ,h\right)$是微波辐射计观测到的视在温度（apparent temperature）或称亮温（brightness temperature），$T_{u}\left( \theta ,h\right)$是大气向上辐射的亮温，$h$是辐射计所在的高度，$\theta$是观测角或卫星天顶角，$e$是海表面的发射率，Ts是海表面的温度，$eT_{s}$等于海面亮温；$T\left(z\right)$是在高度$z$处大气的温度，$K_{ab}$是大气的吸收系数，在微波波段大气的吸收系数与${\rm d}z$的乘积$K_{ab}{\rm d}z$等于在${\rm d}z$路径内大气的吸收率。 $t$代表从海面$0$到高空$h$之间大气层的透射率，它的计算公式是
$$t\left( 0,h\right) =\exp [-\tau \left( 0,h\right)sec\theta]$$
  式中$\tau \left( 0,h\right)$是从海面$0$到高空$h$之间大气层的光学厚度。

  考虑更多的辐射源，适合于微波辐射计的辐射传输方程可表示为（Stewart 1985）
$$T\left( \theta ,h\right) =etT_{s}+T_{u}\left( \theta ,h\right)+\rho tT_{d}+\rho t^{2}\left(T_{gal}+T_{cos}+T_{sun}\right) $$
  式中$T\left( \theta ,h\right)$是微波辐射计观测的视在温度（apparent temperature）或亮温（brightness temperature）；$T_{u}$是大气向上辐射的亮温；$\rho$是海面的菲涅耳反射率；$T_{gal}$ 和$T_{cos}$分别是银河系噪音（galactic noise）等效温度（对于f>3GHz，$T_{gal}$<1K）和宇宙黑体辐射（cosmic blackbody radiation）等效温度（$T_{cos}$≈3K）；$T_{sun}$是太阳表面温度，$ρ t^{2}T_{sun}$代表反射的太阳辐射，辐射计应避免接收到它。对于频率大于3GHz的电磁波，电离层噪音的等效温度很小可以忽略。大气向上辐射的亮温$T_{u}$还可以进一步被简化为
$$T_{u}=e_{A}T_{A}=T_{A}\left(1-t\right)$$

  式中$T_{A}$是某种加权平均大气温度，在估计AMSR通道上水蒸汽引起的衰减系数时，某些文献采用了这种近似（Xia 2001）。在上面的公式中，$e_{A}$是大气的发射率。根据基尔霍夫定律，在大气内部大气的发射率$e_{A}$等于大气的吸收率$a_{A}$，大气的吸收率$a_{A}$与大气的透射率$t$之和等于1。

TRMM/TMI卫星及传感器介绍

装载微波辐射计的卫星

EOS-PM：又名Aqua，是美国的地球观测卫星（下午星），装载着日本高级微波扫描辐射计AMSR-E(advanced microwave scanning radiometer for EOS)。下午卫星(EOS-AQUA)于2002年5月2日成功发射，过境时间为下午14:30和凌晨2:30。采用三轴稳定卫星平台，轨道倾角98.2°，卫星轨道高度705公里。上午星共有星载遥感观测平台5套，依其分辨率的不同，覆盖全球的时间在1天(14.2条轨道)～16天(约233条轨道)一次。

JERS-1： 日本的地球资源卫星卫星，1992年2月11日发射，为太阳同步轨道，其轨道高度：796公里，倾角:97.662o ，运行周期：96.146分钟，重复周期：44天，赤道上空高度：568.023公里 经过降交点的当地时间：10：30-11：00 空间分辨率：方位方向18米。其装载的热带降雨测量任务（TRMM）微波成像仪TMI（TRMM microwave imager）在五个波段设有十个通道
DMSP：全名Defense Meteorological Satellite Program，是美国国防部的极轨卫星计划。运行在高度约830km的太阳同步轨道，周期约101min，扫描条带宽度3 000km。DMSP卫星采用双星运行体制，两颗业务卫星同时运行，过赤道时间为05∶36及10∶52，每6h可提供一次全球云图。其装载的专用传感器微波成像仪SSM/I(special sensor microwave/imager)在四个波段设有7个通道。

TRMM

  TRMM（Tropical Rainfall Measuring Mission）实验计划是美国和日本合作开展的热带降雨测量计划，日本负责提供TRMM卫星的H-2发射火箭和星载关键仪器测雨雷达。美国NASA提供太空舱和PR以外的其他仪器，以及卫星的业务运行系统。卫星的业务控制是通过NASA的“在轨运行和资料无线电转播卫星系统（TDRSS）”来执行的。TRMM卫星于1997年11月28日在日本种子岛（Tanegashima）空间中心发射，轨道高度是350km，属于Circlar轨道。TRMM卫星的仪器有5个：测雨雷达（Precipitation Radar, PR）、微波成像仪（TRMM µwave Imager，TMI）、可见光和红外扫描仪（Visible and Infrared Scanner，VIRS）、云和地球辐射能量系统（Clouds and the Earth Radiant Energy System，CERES）、闪电成像传感器（Lightning Imaging Sensor，LIS）。

TMI

  热带降雨测量卫星(TRMM)上的微波成像仪(TMI)是一个被动微波传感器，目的在于在TRMM卫星下通过宽行迹提供定量的降雨信息。通过对地球和大气层释放的的微量微波能量进行细微的测量，TMI能够定量的测量大气层中的水蒸气，云水量和降雨强度。TMI系以星下点为转轴，面对地球做由左至右，离开星下点49度向前（天顶角约52.8度），作刈幅(swath)直线距离约760公里的锥形模式(conical mode)扫瞄。
  TMI改良自美国地区DMSP卫星SSM/I，与原来相比，增加了10.7GHz频道，并因应热带地区降雨特性，将原22.235GHz频率改为21.3GHz，故其九个微波探测频道，所使用的是10.7、19.4、21.3、37与85.5GHz五个微波波段，其中除了21.3GHz仅有垂直线性极化外，其余均为垂直与水平线性极化频道。
  除了微波成像仪有10.7 GHz.这个通道外，其他频率都是与专用微波成像仪的频率段相似的。10.7 GHz.的通道用来提供热带降雨中常见的高降雨率作出更为线性的反应。比起专用微波成像仪的860公里的高度，热带降雨测量任务卫星的高度只有402公里。微波成像仪在地球表面有878公里的宽刈幅。正是因为TRMM上面TMI的高分辨率和10.7GHz的通道，使得TMI强于之前的任何一个传感器。

TMI反演SST算法

概述与背景资料

  1. 海洋数据的理想恢复精度
  2. 调查目标
      本次调查的主要目标有两个。首先是要发展一个海洋反演算法，该算法反演表1中规定的TS，W，V，和L的精度。这些产物将对地球科学界有着极大的作用。第二个目标是改善海表面和干燥大气的辐射传输模型。AMSR上的6.9和10.7GHz通道将会提供最新RTM低频信息。经验表明，这两个目标之间是精密相连的。由于对RTM有比较深刻的理解，所以检索的结果更加准确，同时也使得新的遥感技术得以产生，例如利用辐射计去测量海表面风矢量。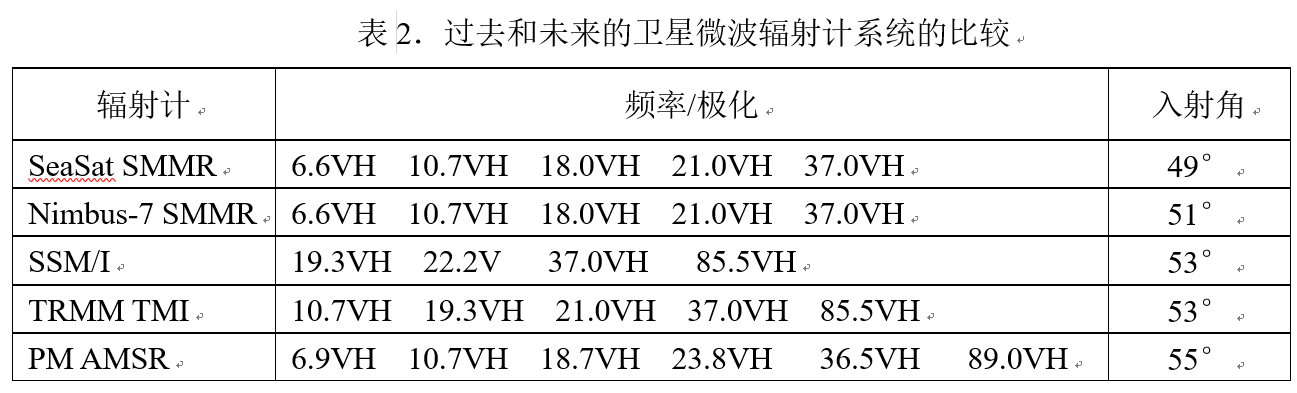

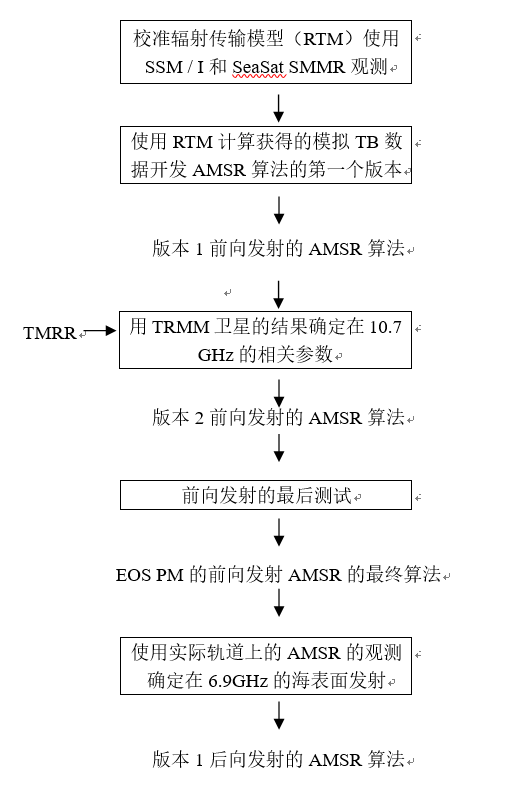
海洋反演算法

  1. 算法类型
    一般来说，有三种类型的海洋反演算法：
    • 多元线性回归算法
    • 非线性迭代算法
    • 后向发射回归算法
        就利用辐射传输理论推导上来说，前两种类型是物理算法。第三类是很少或根本没有考虑基本物理理论的纯粹的统计模型。我们现在描述这些算法并讨论它们的优缺点。
  2. 多元线性回归算法
      在回归分析中，如果有两个或两个以上的自变量，就称为多元回归。事实上，一种现象常常是与多个因素相联系的，由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。因此多元线性回归比一元线性回归的实用意义更大。

  3. 线性回归算法的推导和检验
      下图显示的AMSR线性回归算法的$C_{ij}$系数的推导。首先得合成一张巨大的海洋大气图。利用1987年到1990年这段期间从一些小岛屿上发射的42195个特性控制探空仪对大气进行了规定。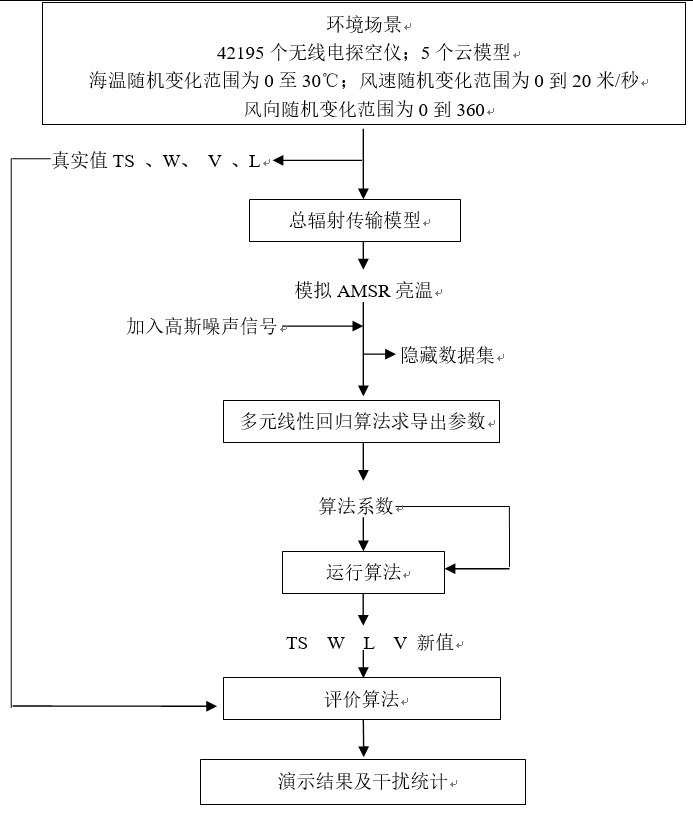

      其中一半探空仪被用于求导的$C_{ij}$系数，另一半被用于测试算法。在探空剖面上叠加了包含密度范围在0—0.3mm的柱状水的一个云层。在这些模拟的大气下面，我们设置了一个粗糙的海表面。海表面温度Ts的随机变化范围0°C-30 °C，风速W的随机变化范围0m/s-20m/s，风向$φ$的随机变化范围0°-360°。利用这个方法获得了大约400000个图像。
      在自然界中，$T_{s}$和W之间有很强的相关性。通过比较图像我们已经证明了这种相关性的存在。例如，我们可能会忽视自然界重来没发生过的水温极低和水蒸气温度极高的情况。然而，现在我们提出这些不切实际的情况是为了确定该算法是否真正能够从V信号中分离出$T_s$信号。
      大气亮温$T_{BU}$、$T_{BD}$和透射率$τ$是把探空仪测的云的概况$T(h)$、$p(h)$、$ρV(h)$、$ρL(h)$带入公式计算出来的。根据上述给出的公式计算出粗糙海面的反射率$R$，来自海表面散射的大气辐射$T_{BΩ}$由公式得到。最后，由AMSR探测到的亮温$T_{B}$关系着大气和海表面。
      把噪声添加到模拟的AMSR的$T_{B}’s$中，代表了其的测量误差。测量误差取决于空间分辨率。在60KM分辨率，对应于6.9GHz的卫星覆盖区，测量误差是0.1K。一个随机数发生器用于产生高斯噪声，这种噪声的标准偏差是0.1 K。这种噪声添加到模拟的AMSR的$T_{B}$中。在模拟过程中，我们还要把模拟错误加到$T_{B}’s$中。模拟错误解释模拟条件和自然条件之间的不同。这是一个很难确定的参数，因为它包含的物理过程在当前的模型中不能被很充分的理解。对于现在来说，我们不能在模拟模型中包含任何建模误差，但是我们会在将来研究这个问题。
      对于已经添加噪音的模拟$T_{B}’s$来说，应用标准的多元线性回归技术可以得出系数$C_{ij}$。这个系数的发现将$P_{j}$ 和实际值的均方根差值在指定的环境场景中减小到了最小值。对于最初的模拟模型的设置，我们应用10个低频通道（即6.9，10.7，18.7，23.8和36.5GHz，双极化），然后我们将通过使用更少的通道来研究其效用。

  4. 非线性迭代算法

  在一般情况下，使用这种方法（非线性迭代算法）并不能保证找到一个合适的解决方案。而且，如果找到了解决方案，也不能保证它是以个独特的解决方案。然而对于AMSR来说，在冷水中，除了36.5GHz通道外在其他通道，∂TB/∂P > 0，$P$和$T_{B}$之间的关系为准线性关系，在36.5GHz通道，$∂T_{B}/∂T_{S} < 0$。经验表明，几乎总能找到一个解决方案。这似乎也表明该解决方案是独一无二的，但是需要验证。

  我们一直假设$T_{B}$与$P$的关系，可以完全由非线性函数模型F来描述。这种情况下，非线性迭代算法对于找到确切的解决方案有独特的优势。相比之下，由线性回归算法得到的$P$将在一定程度上由于非线性而错误。然而，在实践中不可能依照模型函数$F(P)$完全代表$T_{B}$与$P$的关系。例如，$T_{B}$不仅取决于柱状水蒸气含量，还取决于水蒸气的垂直分布。因此，从辐射传输积分方程推导模型函数$F(P)$时，需要作出一些近似。这些假设在第二节进行了讨论。在线性回归算法的推导中，应用了完整的辐射传输积分公式，而且简化假设没有用。比较这两种算法，在由线性回归算法中用非线性关系引起的错误和由非线性迭代算法简化假设引起的错误中存在一个权衡。我们的计划是平行的开发和测试两种算法，比较它们的相对性能，然后选择一个。

IDL读取TRMM/TMI全球SST程序

IDL介绍

  IDL（Interactive Data Language）交互式数据语言是进行二维及多维数据可视化分析及应用开发的理想软件工具。作为面向矩阵、语法简单的第四代可视化语言，IDL致力于科学数据的可视化和分析。
  IDL在海洋领域具有广泛的应用，在各种海洋数据的可视化及与时间、空间相关的分析，对风、流、浪、温度以及水、粒子流等数据的生物学和化学参数的时间序列，不同格式的数据的读取，不同的机器和操作系统的兼容都有很强的优势。

用到主要的IDL过程及函数命令

Openr, readu, congrid, contour, xrange, xstyle, xticks, xtickv,xtickname, tvscl, tv, tvrd(), write\_png。

实验数据：

TMI_2012.zip

编写的主程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
pro TMI\_SST
;打开文件
filename=dialog\_pickfile()
;判断文件是否存在并读取数据
binarydata= bytarr(1440,320,6)
exist=findfile(filename,COUNT=cnt)
if (cnt eq 1) then begin
    close,2
  openr,2,filename, error=err
  if (err gt 0) then begin
    print, 'ERROR OPENING FILE:', filename
  endif else begin
    readu,2,binarydata
    close,2
  endelse
endif
;提取反演SST所用数据
data = binarydata[*,*,0]
data = reform(data)
data = float(data)
;将有效值转换成SST
valid = where(data le 250)
data(valid) = data(valid)*0.15 - 3
;给无效值重新赋值
invalid=where(data gt 250)
data[invalid] = 0
;创建窗口
device,decompose=0
window,/free,xsize=1540,ysize=520,title ='TMI inversion SST image'
;填充背景色
tvlct,200,200,200,1
erase,color=1
;绘制地图
loadct,39
tvscl,data,50,120
;添加坐标
map\_set,0,0,/MERCATOR ,position=[50/1540.0,120/520.0,1490/1540.0,440/520.0] $
,limit=[-40,-180,40,180],/advance,/noerase,title='Sea Surface Temperature (degree C)',charsize=2
map\_grid,/box,latdel=20,londel=25,charsize=0.75,color=1
;添加色标条
colorbar=bindgen(255)#replicate(1b,20)
colorbar=congrid(colorbar,1200,35)
tv,colorbar,170,40
;绘制colorbar的刻度值
plot,indgen(20),/nodata,position=[170/1540.0,40/520.0,1369/1540.0,75/520.0],$
title='the world average sea surface temperature ',xstyle=1,xticks=5,$
xtickv=indgen(6)*7.5-3,xticklen=0.2,ystyle=4,color=1,xminor=10,/noerase
;输出图像
image=tvrd(true=1)
fileout=DIALOG\_WRITE\_IMAGE(image,FILENAME='myimage.png')
END

TMI反演SST结果

TMI反演2012年全球SST12个月的结果：
TMI反演全球SST（2012.1）
TMI反演全球SST（2012.2）
TMI反演全球SST（2012.3）
TMI反演全球SST（2012.4）
TMI反演全球SST（2012.5）
TMI反演全球SST（2012.6）
TMI反演全球SST（2012.7）
TMI反演全球SST（2012.8）
TMI反演全球SST（2012.9）
TMI反演全球SST（2012.10）
TMI反演全球SST（2012.11）
TMI反演全球SST（2012.12）

结论

合成效果图：
合成图
从反演结果来看，可以得出以下结论：

  1. 全球的海表温度分布特点是赤道地区温度最高，随着纬度的升高而降低。且海表温度分布情况随季节变化明显，夏季高温区域像北偏移，冬季南移。春秋季节分布较均匀。这是由于海表面接收到的太阳辐射量沿纬向分布和季节变化造成的。
  2. 由于受加利福利亚寒流和秘鲁寒流的影响，在北美洲西南部海域和南美洲西部海域出现了相比同纬度海表温度较低的现象。
  3. 受到海表面风、海水深度、大陆的影响，部分海表的温度也受到影响，如内陆海，浅水地区的SST容易受外界影响，变化较快。
    海洋是气候系统中的重要组成部分，因其面积广、水量大、热容量大，所以海水温度变化比陆地温度的变化小得多。这就使海洋上空的气温比陆地上空的气温变化慢，因此海水对大气温度起着调节作用。反演SST对于了解全球气候变化有着重要的意义。随着近些年来全球气候不断变暖，监测全球SST就变得尤为重要。

  以往海洋观测主要来自于船舶观测、浮标观测、海岸水文站观测等，这些资料都受到了时间和空间的限制，尤其对广袤的海洋来说，这些有限的资料更本无法满足海洋模式对其的需要。20世纪60年代以来，由于空间科学技术的蓬勃发展，遥感技术飞跃到了一个崭新的阶段，从而引起了海洋信息提取和海洋科学研究一次革命性的变化，为海洋观测开启了新的研究领域。卫星遥感观测资料具有覆盖全球、连续、实时的特点，利用卫星遥感获取还表面温度信息可以得到大面积的同步数据。同时卫星监测还能长时间的连续观测，获取多年资料，这有利于对海洋现象总结，发现海洋中长周期的缓慢变化规律。

  面对全球变暖现象，利用卫星遥感长期观测，可以发现全球气温多年的微变化，为研究全球气候提供重要数据。同时利用卫星遥感反演SST可以实时监测海表温度，及时预报厄尔尼诺现象、拉尼娜现象等海洋异常现象。

若本文对您有帮助，请打赏鼓励本人！
---------------- End ----------------
扫二维码
扫一扫，使用手机查看

扫一扫，使用手机查看

发送邮件
QQ