C#实现定积分求解

在科学研究和实际生产中，经常遇到求积分的计算问题。我们知道在高等数学中，可以通过牛顿-莱布尼兹公式推导原函数的方法求得积分。而本篇博客中将从定积分的物理意义出发，通过原函数的图像的手段来近似地求解给定函数的定积分。

随机投点法（蒙特卡洛算法）

在a到b和函数组成的矩形的范围内，随机投N个点，落到绿色阴影点的个数为M个，对于此图来说便可以容易得知积分的值（绿色阴影）为(M/N)*矩形面积。

考虑到积分的正负性，随机点落到积分面积内时，分为两种情况：当随机点落在x轴上方时，计数加一，随机点落在x轴下方时，计数减一。

private double methodMTK( double upLimit, double lowLimit)
{
    Random randx = new Random();
    Random randy = new Random();
    double result = 0;
    int N = 1000000;  
    int count = 0;
    for (int i = 0; i < N; i++)
    {
        double x = lowLimit + (upLimit - lowLimit) * randx.NextDouble();
        double y = yMin + (yMax - yMin) * randx.NextDouble(); ;
        if (f(x) > 0 && f(x) >= y && y >= 0)
            count++;
        if (f(x) < 0 && f(x) <= y && y <= 0)
            count--;
    }
    result = Math.Abs(((double)count / N) * ((yMax-yMin)*(upLimit-lowLimit)));
    return result;
}

定义法求积分

把一块面积分解成N个小矩形，然后求面积和，最后求极限。我们就利用这种方式来实现它，但我们的N毕竟有限，为了结果更准确，把求矩形面积改成求梯形面积（当然矩形也是可以的），如下图：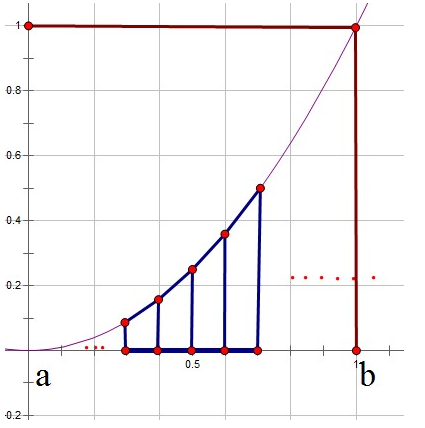

把$\left(a,b\right)$分成$N$等分，积分值等于$S_{1}+S_{2}+….+S_{n}$，其中 $S_{i} = \left(f\left(x_{i}\right) + f\left(x_{i+1}\right)\right) * \left(b-a\right)/n / 2$ (矩形面积公式）。

private double methodDY(double upLimit, double lowLimit)
{
    int N = 1000000;
    double step = (upLimit - lowLimit) / N;
    double result = 0;
    for (int i = 0; i < N; i++)
    {
        result += f(lowLimit+step*i) * step;
    }
    return result;
}

变步长梯形求积分法

用定义求积分法，要确定积分的误差是很难的，我们无法找到一个正好的N值符合我们要求的误差值，所以就需对定义法进行改进，改进的方式就是把原来固定的步长改为变化的步长，利用二分法，如下图：

分到 | 后一个面积和 - 前一个面积和 | < 规定误差 时。这样我们就达到了精确的目的。

private double methodBBCTX(double upLimit, double lowLimit)
{ 
    double e = 0.0000001;
    double s0 = 0;
    double s = 05 * (f(upLimit) + f(lowLimit)) * (upLimit - lowLimit);
    for (int i = 2; Math.Abs(s - s0) > e; i *= 2)
    {
        double h = (upLimit - lowLimit) / i;
        double sum = 0;
        double a = lowLimit;
        for (int j = 0; j < i; j++)
        {
            sum += 0.5 * (f(a) + f(a + h)) * h;
            a = a + h;
        }
        s0 = s;
        s = sum;
    }
    return s0;
}

C#实现

应用程序主界面：

输入

输入参数
如下图所示，标识部分为程序的输入部分，包含以下几个必要的输入参数：
1) 被积函数：该部分为被积函数的表达式，变量需用x表示，如0.5*x、0.5*x+0.25*x*x*x。同时，该部分还支持C#的Math库中的函数，如Math.Sqrt()、Math.Abs()、Math.Tan()等。
2) 积分上限：定积分的积分上限。
3) 积分下限：定积分的积分下限。
4) 积分方法：该应用程序用来求解定积分所使用的算法，包括：蒙特卡洛算法(随机投点法)、定积分定义法、变步长梯形求积分法。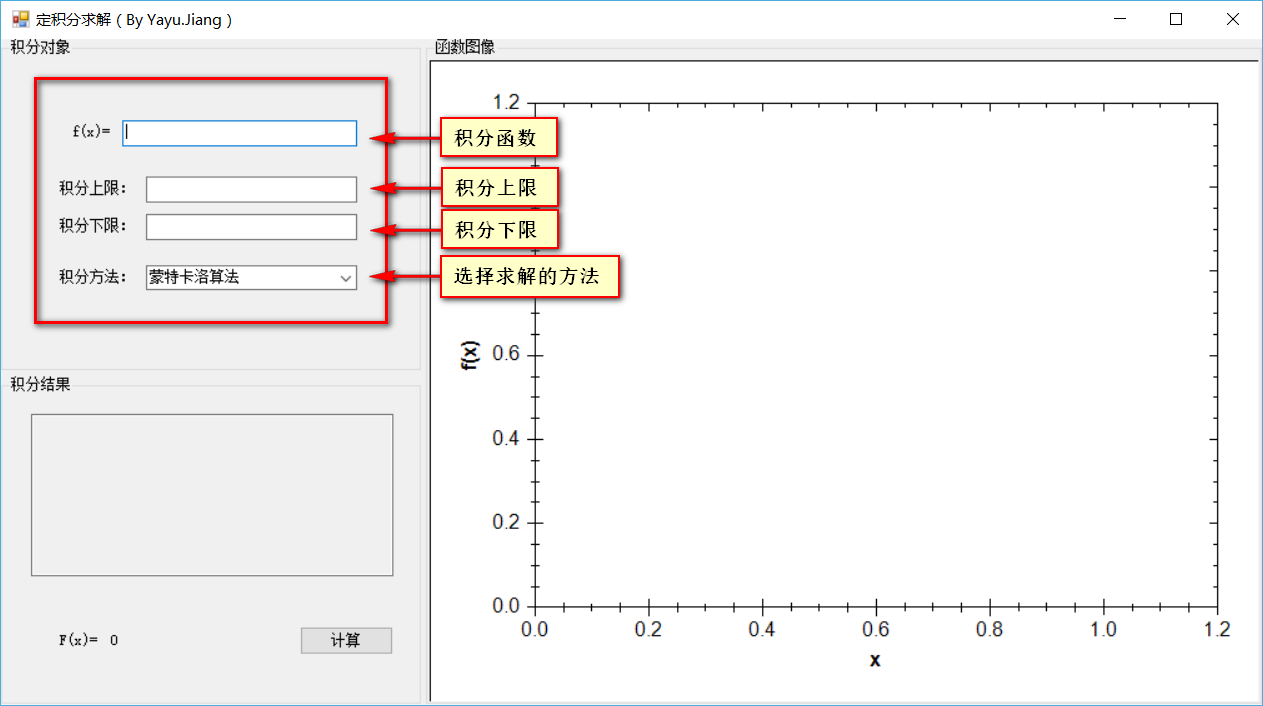

函数表达式的动态编译
由于函数表达式是在程序运行后手动输入的，因此函数表达式不能被当做代码执行。这里提供的解决方案是使用动态编译技术，让函数表达式被动态编译到内存中，供主程序调用，具体实现如下：

 //动态编译代码
 private CompilerResults getCompilerResult(string expression)
 {
     //动态编译函数表达式
     CSharpCodeProvider provider = new CSharpCodeProvider();
     CompilerParameters parameter = new CompilerParameters();
     parameter.ReferencedAssemblies.Add("System.dll");
     parameter.GenerateExecutable = false;       //<--不生成exe
     parameter.GenerateInMemory = true;          //<--直接在内存运行
     CompilerResults result = provider.CompileAssemblyFromSource(parameter, GenerateCodeBlocks(expression));
     //动态编译
     if (result.Errors.Count > 0)
     {
         MessageBox.Show("函数表达式错误！", "Error", MessageBoxButtons.OK);
         return null;
     }
     return result;
 }
 
 //拼接代码块
 private string GenerateCodeBlocks(string formula)
 {
     string code =
         "using System;" +
         "namespace demo" +
         "{" +
            "public static class calculation" +
            "{" +
            "public static double dowork(double x, double y)" +
            "{ return " + formula +
            ";}}}"; //这里是将你的formula和代码片段拼接成完整的程序准备编译的过程。
     return code;
 }
//实现函数表达式求值
 private private double f(double x)
 {
     if (compResult == null)
     {
         return 0;
     }
     else
         return Convert.ToDouble(compResult.CompiledAssembly.GetType("demo.calculation").GetMethod("dowork").Invoke(null, new object[] { x, 0 }));
 }

输出

设置好输入参数后，点击下面的计算按钮，即可使用选定的方法计算所输入定积分的结果：

注：
1)由于是近似求解，其结果与实际定积分的结果有一定偏差，但一般较小，在非精确计算的情况下可以忽略。
2)一般而言，蒙特卡洛算法的精确度随着投点数的增加而越来越接近真实值，但由于本程序兼顾计算效率问题，将投点数设置为1000000，有需要的可以修改。
3)定义法和变步长梯形求积分法在具有较高计算效率的同时有较好的精确度。
4)针对线性函数的定积分求解，由于算法的特性决定变步长梯形求解法效率最高，且没有误差。

显示

本应用程序在计算结果的同时，还能显示被积函数的函数图像：

此处的函数图像的显示使用的是ZedGraph控件,其Sourceforge的下载地址为：https://sourceforge.net/projects/zedgraph/
在点击计算按钮的时候调用绘图函数绘制函数图像，绘图部分的实现如下：

private void Draw(double upLimit,double lowLimit)
{
    zedGraphControl1.GraphPane.CurveList.Clear();
    double[] Xs = new double[1000];
    double[] Ys = new double[1000];
    Xs[0] = lowLimit;
    Ys[0] = f(lowLimit);
    double step = (upLimit - lowLimit) / 1000;
    for (int i = 1; i < 1000; i++)
    {
        Xs[i] = Xs[i - 1] + step;
        Ys[i] = f(Xs[i]);
        yMin = Ys[i] < yMin ? Ys[i] : yMin;
        yMax = Ys[i] > yMax ? Ys[i] : yMax;
    }
    zedGraphControl1.GraphPane.AddCurve("f(x)", Xs, Ys, Color.Blue, SymbolType.None);
    zedGraphControl1.AxisChange();
    zedGraphControl1.Invalidate();
}

GitHub项目地址

https://github.com/Alexander-Chiang/Integrals