迭代法求解线性方程组--C#实现Jacobi、Gauss-Seidel、SOR迭代法

发表于 | 分类于 | 阅读次数

当直接求解方程组 $Ax = b$ 较困难时, 我们可以求解一个近似方程组
$$Mx = b$$
设其解为 $x^{(1)}$
易知它与真解之间的误差满足
$$A\left(x_{*}-x^{(1)}\right) = b-Ax^{(1)}$$
如果 $x^{(1)}$ 已经满足精度要求, 则停止计算, 否则需要修正。

设修正量为$\Delta x$ 显然$\Delta x$满足方程 $A\Delta x = b-Ax^{(1)}$. 但由于直接求解该方程比较困难, 因此我们还是求解近似
$$M\Delta x = b − Ax^{(1)}$$
于是得到修正后的近似解
$$ x^{(2)}= x^{(1)}+\Delta x = x^{(1)}+M^{-1}\left(b-Ax^{(1)}\right) $$
若$x^{(2)}$已经满足精度要求, 则停止计算, 否则继续按以上的方式进行修正。
不断重复以上步骤, 于是, 我们就得到一个序列
$$x^{(1)},x^{(2)},…,x^{(k)},…$$
满足以下递推关系:
$$x^{(k+1)}=x^{(k)}+M^{-1}\left(b-Ax^{(k)}\right), k=1,2,…$$
由于每次迭代的格式是一样的, 因此称为定常迭代。

注：通常, 构造一个好的定常迭代, 需要考虑以下两点:
(1) 以$M$为系数矩阵的线性方程组必须要比原线性方程组容易求解;
(2) $M$应该是$A$的一个很好的近似, 或者迭代序列${x^{k}}$要收敛

C#实现

应用程序界面

  应用程序包含菜单、输入输出、设置和日志模块，如图所示：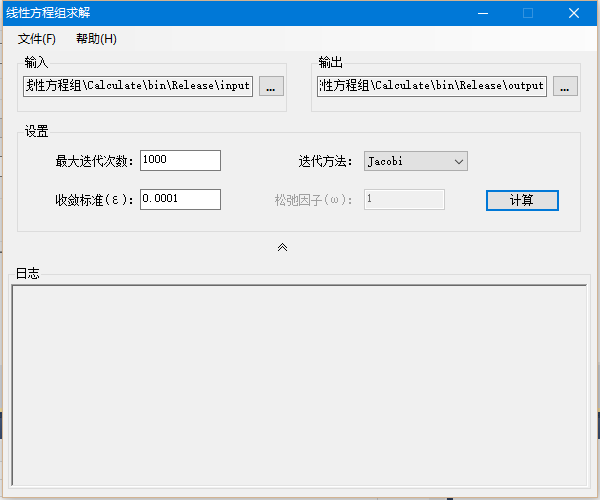

数据说明

  1. 路径说明
      程序启动时，会自动读取所在路径，默认的输入输出路径为应用程序目录下的input和output文件夹(下图所示)。程序计算所需的输入数据存应存放于input文件夹中，最终计算结果将输出到output文件夹中。
    也可以通过修改输入输出路径的方法，重新指定输入数据存放的位置和最终计算结果的输出位置。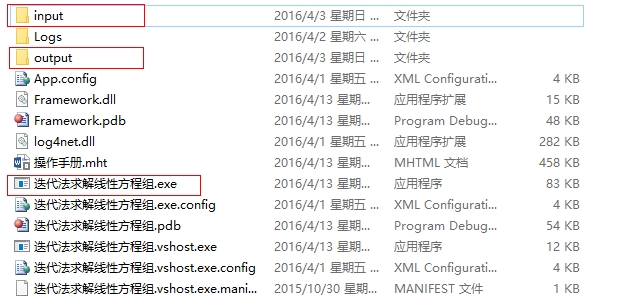
  2. 数据格式
    （1）输入数据
      位于应用程序所在路径下的input文件夹的.txt文本文件，其数据格式为：

    第一行为线性方程组的未知数个数；
    第二行起的数据代表线性方程组系数的增广矩阵，每一行表示一个线性方程。

（2）输出结果
  位于应用程序所在路径下的output文件夹的.txt文本文件，其数据格式为：
从第一行开始分别表示线性方程组的解x1,x2,x3,…的值，最后两行分别标识所使用迭代方法和迭代次数。

参数设置


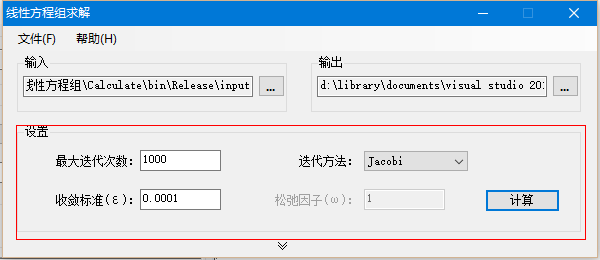
如图所示部分为迭代求解过程中的参数数值的设定，
最大迭代次数：指示迭代过程中，最大迭代的次数。迭代次数超过该值时停止迭代。
收敛标准（ε）:当两次迭代所得数值之差的绝对值均小于某一给定的数ε时，视为已求得近似解。此时停止迭代，输出结果。
(注：以上条件满足其一，即停止迭代。)
迭代方法：求解使用的迭代方法。该程序内置迭代方法有：Jacobi迭代法、Gauss-Seidel迭代法、逐次超松弛迭代法(SOR法)。
松弛因子(ω)：SOR迭代法的参数，一般1<ω<2；

      0<ω<1时，称为亚松弛法；

      ω > 1时，称为超松弛法；

      Ω=1时，即为高斯-塞德尔迭代；

计算说明

（1） 应用程序会遍历输入文件夹中的所有.txt文件，按照指定的数据格式读取文件

读取的输入文件格式为：

第一行为线性方程组的未知数个数；
第二行起的数据代表线性方程组系数的增广矩阵，每一行表示一个线性方程。
（2） 可以根据文件内容生成并显示方程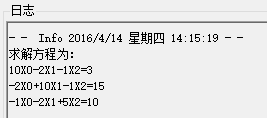

（3） 根据指定的参数和迭代方法求解方程组
（4） 显示求解结果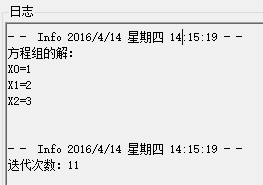

（5） 将最终结果存放至输出文件夹中，并命名为xxx_solution.txt


从第一行开始分别表示线性方程组的解x1,x2,x3,…的值，最后两行分别标识所使用迭代方法和迭代次数。

异常处理

（1） 路径错误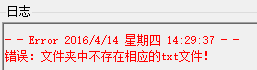

（2） 文件为空

（3） 数据内容错误


（4） 解不收敛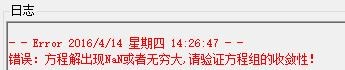

关键步骤代码

迭代部分的源码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
/// <summary>
/// 方程组系数增广矩阵等价变换
/// </summary>
/// <param name="c">输入增广矩阵</param>
/// <returns>等价变换后的增广矩阵</returns>
private static List<double[]>  matTrans(List<double[]> c)
{
    List<double[]> cTrans = new List<double[]>();
    for (int i = 0; i < c.Count; i++)
    {
        double[] ci = new double[c[i].Length];
        c[i].CopyTo(ci, 0);
        if (ci[i] == 0)
        {
            ci = c[i];
            ci[i] = 1;
            ci[ci.Length - 1] = -ci[ci.Length - 1];
        }
        else
        {
            for (int j = 0; j < ci.Length ; j++)
            {
                ci[j] = -ci[j] / c[i][i];
            }
            ci[i] = 0;
            ci[ci.Length - 1] = -ci[ci.Length - 1];
        }
        cTrans.Add(ci);
    }
    return cTrans;
}
/// <summary>
/// Jacobi迭代法求解线性方程组
/// </summary>
/// <param name="c">方程组系数的增广矩阵</param>
/// <param name="IterativeTimes">最大迭代次数</param>
/// <param name="Epsilon">收敛标准</param>
/// <param name="t">迭代次数</param>
/// <param name="solution">求解结果</param>
/// <returns>执行结果，0表示求解成功</returns>
public static int Jacobi(List<double[]> c, int IterativeTimes, double Epsilon, out int t, double[] solution)
{
    List<double[]> cTrans = matTrans(c);
    double[] history = new double[cTrans.Count];
    double[] now = new double[cTrans.Count];
    int times = 0;
    bool isTrueSolution = false;
    while (times <= IterativeTimes && !isTrueSolution)
    {
        //迭代一次
        for (int i = 0; i < cTrans.Count; i++)
        {
            now[i] = 0;
            double[] Con = cTrans[i];
            for (int j = 0; j < Con.Length - 1; j++)
            {
                now[i] += Con[j] * history[j];
            }
            now[i] += Con[Con.Length - 1];
            if (Double.IsNaN(now[i]) || Double.IsInfinity(now[i]))
                throw new Exception("错误：方程解出现NaN或者无穷大,请验证方程组的收敛性！");
        }
        times++;
        //解是否符合条件
        isTrueSolution = true;
        for (int i = 0; i < now.Length; i++)
        {
            if (Math.Abs(now[i] - history[i]) > Epsilon)
            {
                isTrueSolution = false;
                break;
            }
        }
        //更新旧解
        now.CopyTo(history, 0);
    }
    t = times;
    now.CopyTo(solution, 0);
    //超出迭代次数求解失败
    if (times > IterativeTimes) return 1;
    else
        return 0;
}
/// <summary>
/// SOR迭代法求解线性方程组
/// </summary>
/// <param name="c">方程组系数的增广矩阵</param>
/// <param name="IterativeTimes">最大迭代次数</param>
/// <param name="Epsilon">收敛标准</param>
/// <param name="omega">松弛因子</param>
/// <param name="t">迭代次数</param>
/// <param name="solution">求解结果</param>
/// <returns>执行结果，0表示求解成功</returns>
public static int SOR(List<double[]> c, int IterativeTimes, double Epsilon,double omega,  out int t, double[] solution)
{
    List<double[]> cTrans = matTrans(c);
    double[] history = new double[cTrans.Count];
    double[] now = new double[cTrans.Count];
    int times = 0;
    bool isTrueSolution = false;
    while (times <= IterativeTimes && !isTrueSolution)
    {        //一次迭代
        for (int i = 0; i < cTrans.Count; i++)
        {
            now.CopyTo(history, 0);
            now[i] = (1-omega)*history[i];
            double[] Con = cTrans[i];
            for (int j = 0; j < Con.Length - 1; j++)
            {
                now[i] += omega * Con[j] * history[j];
            }
            now[i] += omega * Con[Con.Length - 1];
            if (Double.IsNaN(now[i]) || Double.IsInfinity(now[i]))
                throw new Exception("错误：方程解出现NaN或者无穷大,请验证方程组的收敛性！");
            
        }
        times++;
        //解是否符合条件
        isTrueSolution = true;
        for (int i = 0; i < now.Length; i++)
        {
            if (Math.Abs(now[i] - history[i]) > Epsilon)
            {
                isTrueSolution = false;
                break;
            }
        }
        //更新旧解
        now.CopyTo(history, 0);
    }
    //超出迭代次数求解失败
    t = times;
    now.CopyTo(solution, 0);
    if (times > IterativeTimes) return 1;
    else
        return 0;}
/// <summary>
/// Gauss-Seidel迭代法求解线性方程组
/// </summary>
/// <param name="c">方程组系数的增广矩阵</param>
/// <param name="IterativeTimes">最大迭代次数</param>
/// <param name="Epsilon">收敛标准</param>
/// <param name="t">迭代次数</param>
/// <param name="solution">求解结果</param>
/// <returns>执行结果，0表示求解成功</returns>
public static int Gauss_Seidel(List<double[]> c, int IterativeTimes, double Epsilon, out int t, double[] solution)
{
    return SOR(c, IterativeTimes, Epsilon, 1, out t, solution);
}

GitHub仓库地址

https://github.com/Alexander-Chiang/Solve-Linear-Equations/

若本文对您有帮助，请打赏鼓励本人！
---------------- End ----------------
扫二维码
扫一扫，使用手机查看

扫一扫，使用手机查看

发送邮件
QQ